ONIOM and Its Application
- prativabehera768
- Apr 26
- 2 min read
Quantum theory provides the foundational framework for numerous computational methods used to analyze chemical structures and reactions. The swift advancements in computer hardware and software have enabled the precise study of small to medium-sized molecules using ab initio methods. Density functional theory and semiempirical methods broaden the scope of applications: for instance, semiempirical calculations are typically used for systems with up to about 100 atoms, and can still be applied to molecules with up to approximately 1000 atoms. Nonetheless, many chemical problems remain beyond the reach of current quantum mechanical methods, both now and in the foreseeable future. These challenges include studying chemical reactivity in solvents and biochemical applications like examining the catalytic role of proteins in enzymatic reactions. Describing the solvent or protein explicitly results in very large systems, and applying quantum mechanical potentials in Molecular Dynamics (MD) or Monte Carlo (MC) simulations of such systems exceeds current computational capabilities. Empirical force fields have been successfully used in many MD and MC simulations, but they are inadequate for chemical reactivity problems because they cannot accurately describe the formation or breaking of chemical bonds. This challenge has led to the development of hybrid quantum mechanical (QM) and molecular mechanical (MM) models, which combine the strengths of both quantum and classical approaches. The quantum approach is more versatile and allows the calculation of ground and excited state electronic properties, such as ionization potential or electron affinity, and chemical reactions. QM methods require little to no parametrization (ab initio) or only limited parametrization (semiempirical), whereas the effectiveness of a classical force field relies heavily on the precise calibration of many parameters against experimental reference data. This ensures the reliability and accuracy of a given MM approach but also limits its application to the specific classes of molecules it was designed for. Many force fields surpass simple QM models in accuracy because specially designed potential functions and flexible parameterizations enable a close match to experimental data. Another advantage of MM force fields is their computational efficiency, making them particularly appealing for MD or MC simulations. They are significantly faster than QM methods and require less computational power as the system size increases. The development of hybrid QM/MM approaches is driven by the idea that large chemical systems can be divided into an electronically significant region requiring a quantum mechanical treatment and a remainder that acts primarily in a perturbative manner, allowing for a classical description. The perturbation may be mainly mechanical, such as when the classical region forces the quantum region into a specific geometry, but it may also involve electronic effects like electrostatics and polarization. According to this concept, a chemical reaction is viewed as a transformation involving only the reactive center (QM region), influenced by its surroundings (MM region, such as the solvent or a protein). This concept is clearly aligned with common chemical reasoning. Over the past two decades, several hybrid QM/MM models have been developed, integrating semiempirical, density functional, valence bond, or ab initio Hartree Fock methodologies with widely used force fields. Most reported applications focus on solvation phenomena, while some address biochemical systems, and extended material frameworks.

















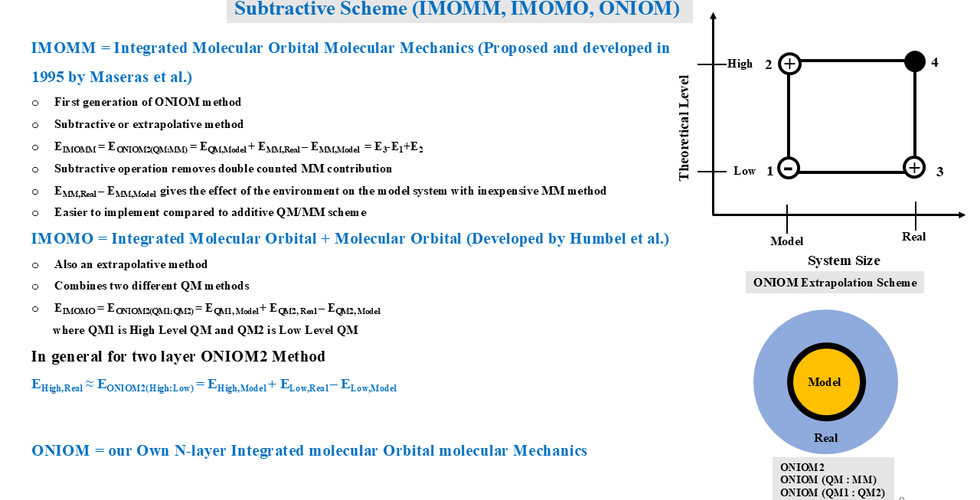

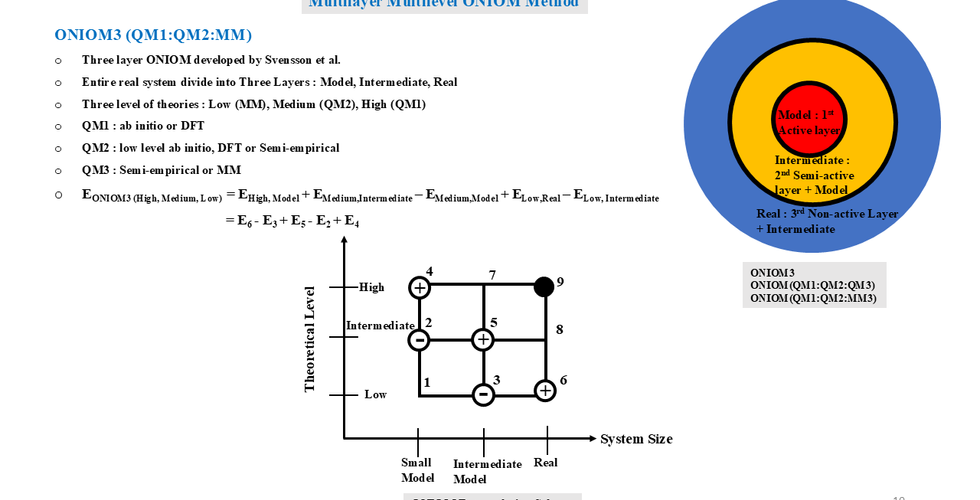

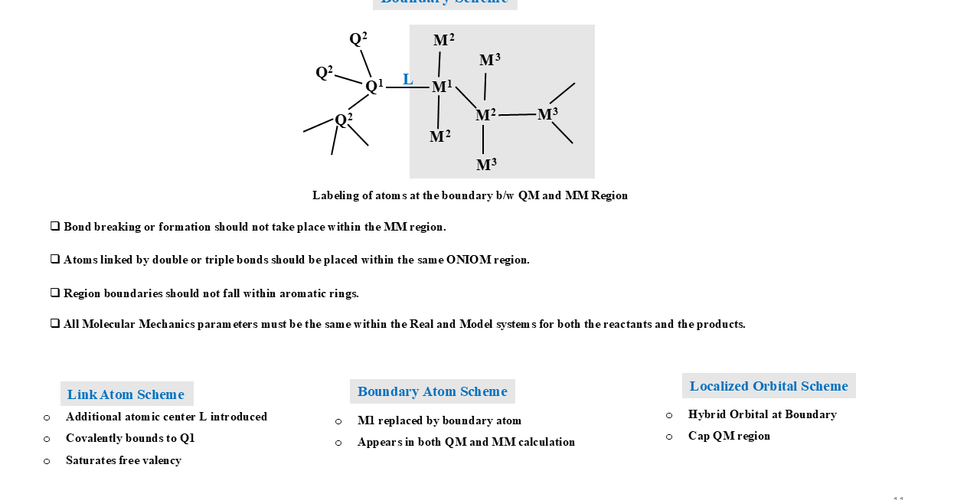
















Comments